Conic Sections (2)

I have installed JavaView. The integration with Mathematica (5.2) is flawless. No further comment on that. The available methods and settings for displaying graphics seem infinite. These pictures are the result of my first try of displaying a Mathematica graphics object with JavaView. The major difference between Mathematica and JavaView is the possibility to interactively modify practically all the object's properties and of course rotating and resizing the object. Go to the JavaView site to get a feel for that.

Conic sections

The circle, ellips, parabola and hyperbola are examples of conic sections:



A conic section is an affine variety like V(x^2 + y^2 - z^2, ax + by + cz). Where x^2 + y^2 - z^2 = 0 is the equation of a cone and ax + by + cz = 0 is the equation of a plane in three dimensional affine space. Depending on the values of a, b and c the affine variety takes the form of a circle, ellips, parabola or hyperbola.

Interesting, not? Let's experiment in Mathematica.

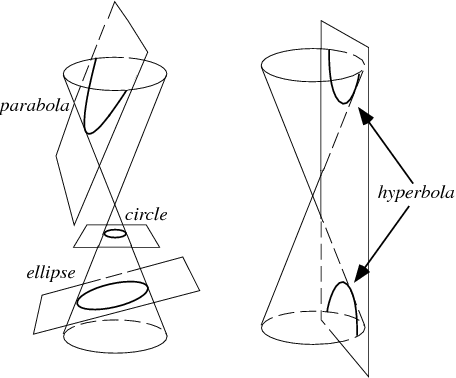
Show[
  ContourPlot3D[x^2 + y^2 - z^2, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}],
  ContourPlot3D[-2x + y - z, {x, -2, 2}, {y, -1, 1}, {z, -2, 2}]
  ]

This images almost asks to be rotated in 3D for further visual inspection. This is where the superb JavaView comes in but that is something for another time.

ImplicitPlot

ImplicitPlot[{y^2\[Equal]x^3-3x+1},{x,-2,2}]

( Elliptic Curve )

Educational software for Abstract Algebra

Exploring Abstract Algebra with Mathematica supports groups, rings and morphisms.


( Example of a visualization of the morphism Z12 -> Z6 )

How to construct this image in Mathematica ?

( What do you think ? )

Quadrifolium (2)

Mathematica plots a quadrifolium if you enter

PolarPlot[Sin[2 theta], {theta, 0, 2Pi}]

Affine Varieties

If V and W ⊂ k^n are affine varieties, then so are V ∩ W and V ∪ W.

Molien's Theorem.

From Appendix D in "Ideals, Varieties, and Algorithms" by Cox, Little, O'Shea.

An interesting project could be built around Molien's Theorem in invariant theory, which is mentioned in §3 of Chapter 7. The algorithm given in STURMFELS (1991) could be implemented to find a set of generators for k[x\, ... ,Xn]^G. This could be applied to find the invariants of some larger groups, such as the rotation group of the cube in R^3. Molien's theorem is also discussed in Chapter 7 of BENSON and GROVE (1985).

Sounds interesting...

Ideals of a field.

I have found a page with a lot of algebra lecture notes of which a few in Dutch. To the point: some new insights I gained today.


Lemma 1:
Let R be a ring and I be an ideal of R. I=R IFF I contains a unit.

Proof:
Assume u is a unit in I. Then R contains an element v such that uv=1. Since I is an ideal uv is in I, or 1 in I. Thus I = <1> = R. Conversely if I = R then I contains the unit 1.


Lemma 2:
A commutative ring R is a field IFF its ideals are {0} and R.

Proof:
Assume I is an ideal of a field R with element u. Since R is a field there is an element v such that uv = 1. Since I is an ideal 1 is in I or I = <1> = R. Conversely, let R have ideals {0} and R. Assume R = (u) and thus 1 in (u) according to Lemma 1. So R has some v such that uv = 1, or every nonzero element in R is a unit and thus R is a field.


Let R,S be rings and f a nonzero ring homomorphism f: R->S. If R is a field then f is injective.

Proof:
According to lemma 2 R has two ideals {0} and R. The ideals are the kernel of a homomorphism. If the kernel of a ring homomorphism is R then it is the zero homomorphism. A homomorphism with kernel {0} is an isomorphism which is injective.

Ideals

(... On Tuesday, June 12, 2007 I wrote:
Let I, J be ideals of Z.
If I=(m), J=(n) then I+J=(GCD(m,n)), and I∩J=(LCM(m,n)). ...)

In fact:
Let I, J be ideals of Z.
If I=(m), J=(n) then
- I*J=(m*n)
- I+J=(GCD(m,n)),
- I∩J=(LCM(m,n)),
- I∪J=I+J.

Example:
I = (6) = {..., -18, -12, -6, 0, 6, 12, 18, 24, ...}
J = (4) = {..., -12, -8, -4, 0, 4, 8, 12, 16, ...}

- I*J={..., -48, -24, 0, 24, 48, 72, ...}
- I+J=(GCD(m,n))={..., -4, -2, 0, 2, 4, 6, ...},
- I∩J=(LCM(m,n))={..., -24, -12, 0, 12, 24, 36, ...},
- I∪J=I+J={..., -4, -2, 0, 2, 4, 6, ...}.

Some progress on Macaulay2 skills

Worked on MT4517 exercises chapter 2.

Show that { a + bX + cX^2 | a,b,c in Z2 and X^3 = 1 + X } is a field and calculate inverses of X, X^2 and 1+X.

Simple.

i96 : describe(R)

ZZ
-- [X]
2
o96 = ----------
3
X  + X + 1


i97 : ( (X)_R )^-1

2
o97 = X  + 1

o97 : R


i98 : ( (X^2) )^-1

2
o98 = X  + X + 1

o98 : R


i99 : ( (1+X)_R )^-1

2
o99 = X  + X

o99 : R

It would be cool to be able to do something like asList(R) where Macaulay2 should reply with 0, 1, 1+X, 1+X^2, etc.

For now I'll do it like this.

i136 : i=0; while i < 7 list (R_0)^i do i = i+1

2          2       2           2
o137 = {1, X, X , X + 1, X  + X, X  + X + 1, X  + 1}

o137 : List

Polynomials

From the Fundamental Theorem of Algebra we know that an n-th degree univariate polynomial has n complex roots.

An example for the case n=3, let x^3+b*x^2+c*x+d=0 have roots r1, r2 and r3. Then

x^3+b*x^2+c*x+d=(x-r1)*(x - r2)*(x - r3),

expanding the right side of this equation gives

x^3+b*x^2+c*x+d=x^3-(r1+r2+r3)*x^2+(r1*r2+r1*r3+r2*r3)*x-r1*r2*r3.

This shows that the coefficients of an n-th degree univariate polynomial are multivariate polynomials in its roots.

Because changing the order of the roots does not change the coefficients the polynomials

-(r1+r2+r3),

(r1*r2+r1*r3+r2*r3) and

-r1*r2*r3,

are symmetric, and are called s(1), s(2) and s(3), or the elementary symmetric functions for n=3.

Algebraic Geometry

What are all these 'advanced' topics in math about? Is it at all possible for an undergraduate to get an idea about, say, what algebraic geometry is all about? It's possible but it requires some searching.



Introduction to Algebraic Geometry

Groupring has zero divisors.

Let R be a ring, G a finite abelian group, RG the groupring of R and G, then RG has zero divisors.

Proof:
Let g be an element of G with order m. Now calculate:
(1-g)*(1+g+g^2+...+g^(m-1) =
( 1+g+g^2+...+g^(m-1) ) - ( g+g^2+...+g^m ) =
1 - g^m = 1 - 1 = 0.

(1-g) is a zero divisor.

Quadrifolium

A surprising result. The area of the four-leaved rose or quadrifolium is half of the circle surrounding it. The area of the circle is pi r^2, while both the blue and yellow areas are 1/2 pi r^2. ( I leave the proof as an exercise. )