Bézout's Theorem

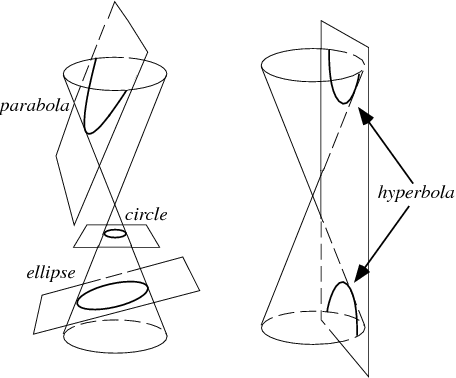
Let a and b be integers with greatest common divisor d. Then there exist integers r and s such that d = ar + bs. Thus, the greatest common divisor of a and b is an integer linear combination of a and b.

( Didn't know that this theorem was called Bézout's Theorem. )

Same topic, different book.

I am studying "Knapp, Basic Algebra", at first read, a well to do self-study book. Chapter I looks like this.
1. Division and Euclidean Algorithms 1
2. Unique Factorization of Integers 4
3. Unique Factorization of Polynomials 9
4. Permutations and Their Signs 15
5. Row Reduction 19
6. Matrix Operations 24
7. Problems 30

A manageable 14 pages on the Euclidean Algorithm for integers and polynomials, but dense. Too dense perhaps. Then I had a look at this other book. "Irving, Integers, Polynomials and Rings", have a look at the table of contents.

1 Introduction: The McNugget Problem
Part I Integers
2 Induction and the Division Theorem
3 The Euclidean Algorithm
4 Congruences
5 Prime Numbers
5.1 Prime Numbers and Generalized Induction
5.2 Uniqueness of Prime Factorizations
5.3 Greatest Common Divisors Revisited
6 Rings
7 Euler’s Theorem
8 Binomial Coefficients
Part II Polynomials
9 Polynomials and Roots
10 Polynomials with Real Coefficients
11 Polynomials with Rational Coefficients
12 Polynomial Rings
13 Quadratic Polynomials
14 Polynomial Congruence Rings
Part III All Together Now
15 Euclidean Rings
16 The Ring of Gaussian Integers
17 Finite Fields

I'll guess I stop for a while on my route and do a bit of fun-studying in Irving. If I don't study it now I probably never will. It is a beautiful book. I was almost forgotten that I had it.

Moebius transformations video

( This video has been watched over a million times on YouTube. )
( Update: 10/4-'10 Added Complex Analysis tag. )

Burnside's Lemma

Burnside's Lemma as it can be found on MathWorld:

Let J be a finite group and the image R(J) be a representation which is a homomorphism of J into a permutation group S(X), where S(X) is the group of all permutations of a set X. Define the orbits of R(J) as the equivalence classes under x~y ,which is true if there is some permutation p in R(J) such that p(x)=y. Define the fixed points of p as the elements x of X for which p(x)=x. Then the arithmetic mean number of fixed points of permutations in R(J) is equal to the number of orbits of R(J).

Today I deepened my understanding of Burnside's Lemma considerably.

The Ascent of Man

Jacob Bronowski: A mathematician turned biologist

An IMDB user wrote about The Ascent of Man:

This remarkable series, thirteen fifty-minute episodes, is one of television's highest achievements. Jacob Bronowski takes the viewer literally around the world, to discuss Mankind's greatest accomplishments and lowest depths. One outstanding quality of this extraordinary series is that Bronowski speaks to the viewer directly, in a very personal fashion, through the lense of the camera.

The book, that derives from the episodes themselves, is a virtual transcript of Bronowski's remarks. These are not "lectures', but rather discussions presenting his "personal view." The episodes are sprinkled with delightful and moving anecdotes of people Bronowski knew and worked with, such as Leo Szilard (who first thought of the nuclear "chain reaction") and John von Neumann (the "Father of Electrionic Computing").

Anyone interested in the history of science - and of thought in general - will be astonished, delighted and deeply moved by "The Ascent of Man." The production value is of the highest order throughout.

Highest recommendation.

ASCENT OF MAN LINKS
- Museum of Broadcasting
- IMDB
- Digitally Remastered series on DVD

Many years ago when I was a school dropout without any qualification whatsoever I thought there was nothing interesting to learn. This series is part of what brought me back on track. I thought about it many times. I wanted to see it again just to check if I still like it, if it still makes an impression. I couldn't find it for many years because I was forgotten the series name, even Bronowski's name. But I wasn't forgotten Bronowski's face, voice and the way he lectures. I found the series by accident. It's on internet if you know where to look. I have episodes 1 to 8 and 9 to 13 soon. Sofar I have seen episode 1. Yes. It is great television. Well worth the time.

Conjugate permutations

Two permutations are conjugate IFF they have the same cycle structure.

So if we calculate the conjugate of
a=(1 2 3)(4 5) and
b=(3 5),
then we know that the conjugate has the same cycle structure as a. Let's find out:
a^b=(3 5)((1 2 3)(4 5))(3 5)
1 2 3 4 5
1 2 5 4 3 : (3 5) applied
2 5 1 3 4 : (1 2 3)(4 5) applied
2 5 4 3 1 : (3 5) applied
In cycles: (1 2 5)(3 4)

There is a smarter way to get at this result. Permute the cycle structure of a with b:
(1 2 3)(4 5)
(1 2 5)(4 3) = (1 2 5)(3 4).

Using this method we can simply find the conjugating permutation of a and b.
For example
a=(1 2 3)(4 5 6) and
b=(1 3 5)(2 4 6).
Since a and b have the same cycle structure there must be a permutation c such that
a=c b c^-1.
1 2 3 4 5 6 : cycle a as permutation
1 3 5 2 4 6 : cycle b as permutation
We get from a to b by applying cycle
(2 3 5 4) which must be c.
Let's verify.

1 2 3 4 5 6
1 3 5 2 4 6 : apply c
3 5 1 4 6 2 : apply b
3 4 5 6 1 2: apply c^-1 = (2 4 5 3)
In cycles:(1 3 5)(2 4 6) = b.

Representations and Characters of Groups

I found an electronic version of a book with a high position on my Amazon wish list. With 458 pages including about 60 pages of worked out solutions of all the exercises it is an excellent source for the self-study of this fascinating topic. I started on Representation Theory, A First Course by Fulton a while ago but after a few chapters it turned out I wasn't ready for all but parts of the book. My intrest in the subject was firmly set.
In the very beginning of my IT "career" ( since I am still on the first step of the corporate ladder it is clear that I am not the typical corporate type of guy, i adjust enough to be able to survive ) I moved to the position of project leader fast. After a year or two I wanted to write a program but I discovered that the languages I could code in ( Databus, Cobol and RPG-II) were dead or not easily available to me. I had to start from scratch. These things don't happen in mathematics, I suppose. I can imagine similar developments in physics though. Imagine string theory to be proved false. If you are a string theory professor you have to come up with something else.
I thought about this when I read "... This set of lecture notes presents a new approach to the representation theory of the symmetric group — more precisely: to the character theory of the symmetric group over a field of characteristic zero ..." in the following book.

Another exercise

My next challenge.

Ken Ward's Math Pages

I read "... to our wives ..." on the first page of "Sequences" by H. Halberstam and K.F. Roth. { Aik. } Ok, printed in 1966. Only fourteen years after Alan Turing was convicted for having a homosexual relationship with a young Manchester man. So maybe "... to our wives ..." means "we are not homosexuals"? Perhaps, not likely. Still, I think it is rather odd to start a mathematics book with "... to our wives ...". Unless it were the wives who were doing the actual mathematics, of course. In that time women were badly discriminated in the academic world. Serious, why write "... to our wives ..." in a mathematics book? Love? Not a very romantic place to put it. A math book! Come on. I think they wrote it out of relief. "... despite your continuous attacks on our concentration by your endless babble talk, loud hoovering and yelling on the phone ..." we managed to finish our book. Something like that.

I added Ken Ward's Math Pages to the Cool Sites box. Although not even close to Eric Weisstein's huge encyclopedic MathWorld I like "Ken's pages" because it has unique content, is the only place on internet where I found a detailed proof of the Vandermonde Convolution theorem, and because I want to create something similar. Different topics of course but of the same ( achievable ) size and quality. Some day this mathematics diary should evolve into a mathematics site with worthwile content.

Impossible Triangle

What did I just see?!

PSTricks

( This morning I asked the account manager what his gut feeling was about the job for which I was interviewed last week. He had an 80% feeling about it. I was more worried because the relationship between the prospect and us was very thin. All we had done was acting upon a request which had been sent to probably every IT company in the country. My position is still 'idle' )

Eventually I want to be able to write mathematics of my own. Besides being able in math, writing math requires some special computer skills. Mathematics is usually not written with a word processor although Word has a nice formula editor nowadays. Writing beautiful mathematics is possible but at the cost of a steep learning curve. The tools to know are MiKTeX and TeXnicCenter. But what about illustrations? For that I discovered an amazing set of tools. PSTricks and LaTeXDraw. PSTricks is a set of commands to include graphics into TeX. LaTeXDraw is a wysyiwig graphics to PSTricks converter. Seeing is believing. This toolset makes it possible to add professional looking graphics to your documents. I think it is worth the steep learning curve. For common graphics a wealth of examples is available anyway.

Exercise ( Aigner ) 1.21

The exercise above is from the book .

I worked on this exercise for a great deal of the week.



I had considerably more time to do math this week. In a sense I even made some discoveries. At least for myself. I am going to try to document them in 'paper-format' during the weekend. If all goes well, I''ll publish them there.

I had time to go after new books as well. Too many topics fascinate me. I want to select a topic in math to which I could eventually contribute. That means that I must be good at it, i.e. find it easily accessible. Becoming 'current' is the first step, I suppose, being able to read the journals and understanding who is who in the world of mathematics. At the moment I am going in the direction of computational group theory, representation theory and combinatorics. Still much too broad, I know.

As far as computational tools are concerned up until now I have worked with GAP and Mathematica. Since a year or so GAP can be used as part of SAGE, a more or less complete math workbench, comparable with Mathematica. The philosophy of the SAGE team is 'best of breed', if I understood them correct. Where Mathematica has to develop all their tools with their own payrolled staff, SAGE draws the best of breed from the Open Source Community, i.e. GAP for Group Theory in SAGE. I don't see Mathematica overtaking the lead from GAP real soon and the same is true for other specialized areas like for example Commutative Algebra. But as a productivity tool Mathematica beats SAGE by far.

Another identity in Pascal's Triangle

On the Pascal Triangle resources website I found, among many other identities, the following two basic identities:

The first one is in every book on discrete math I have seen thus far. And although basic I don't recall to have seen the second identity somewhere else so for me it is a new one.

Michael Pogorsky's proof of Fermat's last theorem

Every now and then I ask the guru's at PlanetMath for help. I did so again today and while I was there I visited the Cafe section in the forum. There was a discussion with a rather long thread about Fermat's last theorem. Because Andrew Wiles proved the theorem with late 20th century mathematics people are still trying to prove the theorem using mathematics from Fermat's days. Every now and again a proof comes up. Usually professional mathematicians don't even bother to look. The mostly unknown authors are called crackpots in mathematical circles. How do these so called 'proofs' look like? Like this for example. It's a proof of Fermat's last theorem by Michael Pogorsky. - Read an analysis of the proof by a PM guru here.

Property of the Pascal Triangle

Another interesting property of the Pascal Triangle.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1

Since Choose(n,k) = (k+1)/(n-k)*Choose(n,k+1) we get ( for example ) for row 7:
1/7 * 7 = 1
2/6 * 21 = 7
3/5 * 35 = 21
4/4 * 35 = 35
5/3 * 21 = 35
6/2 * 7 = 21
7/1 * 1 = 7

Wolfram 2,3 Turing Machine

News update from Mathematica:

We're excited to announce that the $25,000 Wolfram 2,3 Turing Machine Research Prize has been won.

Alex Smith, a 20-year-old undergraduate in Birmingham, UK, has given a 40-page proof that Wolfram's 2,3 Turing machine is indeed universal.

This result ends a half-century quest to find the simplest possible universal Turing machine.

It also provides strong further evidence for Wolfram's Principle of Computational Equivalence.

The official prize ceremony is planned for November at Bletchley Park, UK, site of Alan Turing's wartime work.

For more information about the prize and the solution, see: http://www.wolframprize.org

Stephen Wolfram has posted his personal reaction to the prize at:
http://blog.wolfram.com/2007/10/the_prize_is_won_the_simplest.html

I am still reading the biography of Alan Turing. I am reading chapter 6 now. World war II has ended and Alan is writing a proposal to get a project for building a general purpose computer ( the first one ever ) funded. He wrote his paper on the Universal Turing Machine long before the war started.

Program for printing a Pascal Triangle:

Using Mathematica ( what else? ):

Pascal[n_]:=MatrixExp[Table[If[i == (j+1),j+1,0],{i,0,n},{j,0,n}]]

Usage: Pascal[n]//MatrixForm

Pascal's Triangle as a Matrix Exponential

For me, this is an amazing result. When I read about it in "Accessing Bernoulli-Numbers by Matrix-Operations, Gottfried Helms 3'2006 Version 2.3" I immediately started Mathematica and tried it myself. The picture above is the result. It's what I call some deep mathematics, although the formula for calculating the Matrix Exponential is easily understood.

Dangerous Knowledge

Dangerous Knowledge is a BBC Four documentary about the lives and work of Georg Cantor, Kurt Godel and Alan Turing. ( Find it on Google Video. ) Cantor, Godel and Turing worked on paradoxical stuff. The paradox about the documentary is that it is about mathematics without showing any of it. I suppose it is a nice documentary if you are familiar with Cantor, Godel and Turing. The documentary in that respect becomes a " complementary ".

Sequences

Sequence
Closed form(ula)
Generating function

{1,1,1,1,...}
a(n)=1
f(x)=1/(1-x)

{1,2,4,8,...}
a(n)=2^n
f(x)=1/(1-2x)

{0,0,0,0,1,1,...}
if (n<4) then a(n)=0 else a(n)=1
f(x)=x^4/(1-x)

See also the Mathematica package RSolve

Generating Functions

Generating functions are one of the most surprising, useful, and clever inventions in discrete mathematics.

Generating functions transform problems about sequences into problems about functions.
For example:
* sequence {1, 4, 9, 16, 25, ... }
* closed form a(n) = n^2
* generating function: F(x)=x(1+x)/(1-x)^3.
Interested? An introduction to generating functions (pdf document) can be found [ here ].

Difference sequences

Rather early in our math education we learn about functions and derivative functions.

  
              f(x+h)-f(x)
f'(x) = lim   -----------
         h-> 0    h 

For example: 
f(x) = x^n
f'(x) = n*x^(n-1)

Something similar can be defined for sequences, in that case the 'derative' is called the difference sequence.

a_n = {1, 16, 81, 256, ... }
f(n) = n^4
f'(n) = 1 + 4n + 6n^2 + 4n^3
f''(n) = 14 + 24n + 12n^2
f(3)(n) = 36 + 24n
f(4)(n) = 24

For an arbitrary sequence f:
f(m)(n) = Sum[(-1)^(k)*Binomial[m,k]*f[n-k+m],{k,0,m}]

Here also we see that Pascal's Triangle has a crucial meaning.

Binomial Theorem

(x + y)^n = Sum(n,k) Choose(n,k) * x^(n-k) * y^k

So what? I can now -prove- it. ( By induction. )

Literary Mathematics

"... A generating function is a clothesline on which we hang up a sequence of numbers for display. ..." ( by Herbert S. Wilf in Generatingfunctionology )

Matrices and the Pacal Triangle

Create a matrix from the first n rows of the Pascal Triangle like

1 0 0 0
1 1 0 0
1 2 1 0
1 3 3 1

Then the inverse of this matrix is...

1 0 0 0
-1 1 0 0
1 -2 1 0
-1 3 -3 1

Discrete Mathematics Using Latin Squares

A truly beautiful mathematics book. A book that demands to be read, studied, worked! I will. I love it already. Happiness is easy.

In the past two decades, researchers have discovered a range of uses for Latin squares that go beyond standard mathematics. People working in the fields of science, engineering, statistics, and even computer science all stand to benefit from a working knowledge of Latin squares. Discrete Mathematics Using Latin Squares is the only upper-level college textbook/professional reference that fully engages the subject and its many important applications.

Fibonacci sequence in the Pascal triangle

Where is the Fibonacci sequence in the Pascal triangle?

1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1

Count as follows.
Start left with a 1.
While on a number:
- Move right
- Move up
- Add to running total.

Let's go.
First row.
1.
Stop.

Second row.
1
Stop.

Third row.
1, right, up
1
Stop.

Fourth row
1, right, up
2
Stop.

Fifth row
1, right, up
3, right, up
1
Stop.

Sixth row
1, right, up
4, right, up
3
Stop.

Totals were 1, 1, 2, 3, 5, 8.

Fibonacci sequence, obvious.

Now what's the proof?

Discrete Mathematics video

I watched video 11-15-00: Combinations and permutations. A lecture by Shai Simonson. A lecture in the Discrete Mathematics series on the ADUni.org website.

Topics:
Counting principles.
- Multiplication
- Addition
- Complement
- Counting double
- 'When are things the same'?
Permutation
Combination
n Choose k.
Binomial Theorem
Pascal Triangle
Proofs
- by formula
- by induction
- by combinatorial argument

Doing proofs by combinatorial argument is a powerful technique. The basic identity from the Pascal triangle
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
...
[n,k]=[n-1,k-1]+[n-1,k]
for example
[6,3]=[5,2]+[5,3]=20=10+10
can easily proven by a combinatorial argument.

Such an argument could be the following.
Let n be the number of employees of a small company with one director. We have to select a k-member team from all employees. The number of teams is [n,k]
Exclude the director from selection and select a k-member team. The number of teams is [n-1,k].
Now select a (k-1)-team, the number of teams is [n-1,k-1] and add the director to it which makes it a k-member team including the director.
Adding the number of k-member teams without a director and k-member teams with a director is the total number of k-member teams or [n-1,k] + [n-1, k-1].

This proves [n,k]=[n-1,k-1]+[n-1,k].

1935

From: Alan Turing, the Enigma by Andrew Hodges, page 94.

He was still only twenty-two. The fellowship carried with it GBP 300 a year for three years, which would normally be extended to six, and no explicit duties. He was entitled to room and board when he chose to reside at Cambridge, and to dine at High Table.

Alan Turing's biography reads like a thriller, situated in the era of Brideshead Rivisited. I am now close to the point where he starts thinking about his (Turing) machines.

Pythagoras' Theorem

a^2 + b^2 = c^2

Play a few times with [ this applet ] and I promise you'll never forget the proof of Pythagoras' Theorem again. Ok, just one of the dozens of proofs, but the proof in the applet is the original one. The requirements for understanding the proof are 1) the formula for the area of a triangle: area = ( base * height )/2 and 2) the area of a triangle does not change if the triangle is rotated.

Conic Sections (2)

I have installed JavaView. The integration with Mathematica (5.2) is flawless. No further comment on that. The available methods and settings for displaying graphics seem infinite. These pictures are the result of my first try of displaying a Mathematica graphics object with JavaView. The major difference between Mathematica and JavaView is the possibility to interactively modify practically all the object's properties and of course rotating and resizing the object. Go to the JavaView site to get a feel for that.

Conic sections

The circle, ellips, parabola and hyperbola are examples of conic sections:



A conic section is an affine variety like V(x^2 + y^2 - z^2, ax + by + cz). Where x^2 + y^2 - z^2 = 0 is the equation of a cone and ax + by + cz = 0 is the equation of a plane in three dimensional affine space. Depending on the values of a, b and c the affine variety takes the form of a circle, ellips, parabola or hyperbola.

Interesting, not? Let's experiment in Mathematica.

Show[
  ContourPlot3D[x^2 + y^2 - z^2, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}],
  ContourPlot3D[-2x + y - z, {x, -2, 2}, {y, -1, 1}, {z, -2, 2}]
  ]

This images almost asks to be rotated in 3D for further visual inspection. This is where the superb JavaView comes in but that is something for another time.

ImplicitPlot

ImplicitPlot[{y^2\[Equal]x^3-3x+1},{x,-2,2}]

( Elliptic Curve )

Educational software for Abstract Algebra

Exploring Abstract Algebra with Mathematica supports groups, rings and morphisms.


( Example of a visualization of the morphism Z12 -> Z6 )

How to construct this image in Mathematica ?

( What do you think ? )

Quadrifolium (2)

Mathematica plots a quadrifolium if you enter

PolarPlot[Sin[2 theta], {theta, 0, 2Pi}]

Affine Varieties

If V and W ⊂ k^n are affine varieties, then so are V ∩ W and V ∪ W.

Molien's Theorem.

From Appendix D in "Ideals, Varieties, and Algorithms" by Cox, Little, O'Shea.

An interesting project could be built around Molien's Theorem in invariant theory, which is mentioned in §3 of Chapter 7. The algorithm given in STURMFELS (1991) could be implemented to find a set of generators for k[x\, ... ,Xn]^G. This could be applied to find the invariants of some larger groups, such as the rotation group of the cube in R^3. Molien's theorem is also discussed in Chapter 7 of BENSON and GROVE (1985).

Sounds interesting...

Ideals of a field.

I have found a page with a lot of algebra lecture notes of which a few in Dutch. To the point: some new insights I gained today.


Lemma 1:
Let R be a ring and I be an ideal of R. I=R IFF I contains a unit.

Proof:
Assume u is a unit in I. Then R contains an element v such that uv=1. Since I is an ideal uv is in I, or 1 in I. Thus I = <1> = R. Conversely if I = R then I contains the unit 1.


Lemma 2:
A commutative ring R is a field IFF its ideals are {0} and R.

Proof:
Assume I is an ideal of a field R with element u. Since R is a field there is an element v such that uv = 1. Since I is an ideal 1 is in I or I = <1> = R. Conversely, let R have ideals {0} and R. Assume R = (u) and thus 1 in (u) according to Lemma 1. So R has some v such that uv = 1, or every nonzero element in R is a unit and thus R is a field.


Let R,S be rings and f a nonzero ring homomorphism f: R->S. If R is a field then f is injective.

Proof:
According to lemma 2 R has two ideals {0} and R. The ideals are the kernel of a homomorphism. If the kernel of a ring homomorphism is R then it is the zero homomorphism. A homomorphism with kernel {0} is an isomorphism which is injective.

Ideals

(... On Tuesday, June 12, 2007 I wrote:
Let I, J be ideals of Z.
If I=(m), J=(n) then I+J=(GCD(m,n)), and I∩J=(LCM(m,n)). ...)

In fact:
Let I, J be ideals of Z.
If I=(m), J=(n) then
- I*J=(m*n)
- I+J=(GCD(m,n)),
- I∩J=(LCM(m,n)),
- I∪J=I+J.

Example:
I = (6) = {..., -18, -12, -6, 0, 6, 12, 18, 24, ...}
J = (4) = {..., -12, -8, -4, 0, 4, 8, 12, 16, ...}

- I*J={..., -48, -24, 0, 24, 48, 72, ...}
- I+J=(GCD(m,n))={..., -4, -2, 0, 2, 4, 6, ...},
- I∩J=(LCM(m,n))={..., -24, -12, 0, 12, 24, 36, ...},
- I∪J=I+J={..., -4, -2, 0, 2, 4, 6, ...}.

Some progress on Macaulay2 skills

Worked on MT4517 exercises chapter 2.

Show that { a + bX + cX^2 | a,b,c in Z2 and X^3 = 1 + X } is a field and calculate inverses of X, X^2 and 1+X.

Simple.

i96 : describe(R)

ZZ
-- [X]
2
o96 = ----------
3
X  + X + 1


i97 : ( (X)_R )^-1

2
o97 = X  + 1

o97 : R


i98 : ( (X^2) )^-1

2
o98 = X  + X + 1

o98 : R


i99 : ( (1+X)_R )^-1

2
o99 = X  + X

o99 : R

It would be cool to be able to do something like asList(R) where Macaulay2 should reply with 0, 1, 1+X, 1+X^2, etc.

For now I'll do it like this.

i136 : i=0; while i < 7 list (R_0)^i do i = i+1

2          2       2           2
o137 = {1, X, X , X + 1, X  + X, X  + X + 1, X  + 1}

o137 : List

Polynomials

From the Fundamental Theorem of Algebra we know that an n-th degree univariate polynomial has n complex roots.

An example for the case n=3, let x^3+b*x^2+c*x+d=0 have roots r1, r2 and r3. Then

x^3+b*x^2+c*x+d=(x-r1)*(x - r2)*(x - r3),

expanding the right side of this equation gives

x^3+b*x^2+c*x+d=x^3-(r1+r2+r3)*x^2+(r1*r2+r1*r3+r2*r3)*x-r1*r2*r3.

This shows that the coefficients of an n-th degree univariate polynomial are multivariate polynomials in its roots.

Because changing the order of the roots does not change the coefficients the polynomials

-(r1+r2+r3),

(r1*r2+r1*r3+r2*r3) and

-r1*r2*r3,

are symmetric, and are called s(1), s(2) and s(3), or the elementary symmetric functions for n=3.

Algebraic Geometry

What are all these 'advanced' topics in math about? Is it at all possible for an undergraduate to get an idea about, say, what algebraic geometry is all about? It's possible but it requires some searching.



Introduction to Algebraic Geometry

Groupring has zero divisors.

Let R be a ring, G a finite abelian group, RG the groupring of R and G, then RG has zero divisors.

Proof:
Let g be an element of G with order m. Now calculate:
(1-g)*(1+g+g^2+...+g^(m-1) =
( 1+g+g^2+...+g^(m-1) ) - ( g+g^2+...+g^m ) =
1 - g^m = 1 - 1 = 0.

(1-g) is a zero divisor.

Quadrifolium

A surprising result. The area of the four-leaved rose or quadrifolium is half of the circle surrounding it. The area of the circle is pi r^2, while both the blue and yellow areas are 1/2 pi r^2. ( I leave the proof as an exercise. )

Macaulay 2

Today I installed Macaulay 2, 'software system devoted to supporting research in algebraic geometry and commutative algebra'.

Example 1: calculate (x+y)^2 in the polynomial ring Z[x,y].

i107 : R=ZZ[x,y]
o107 = R
o107 : PolynomialRing
i108 : (x+y)^2
        2           2
o108 = x  + 2x*y + y
o108 : R

Example 2: calculate (x+y)^2 in the polynomial ring Z/2[x,y].

i111 : R=ZZ/2[x,y]
o111 = R
o111 : PolynomialRing
i112 : (x+y)^2
        2    2
o112 = x  + y
o112 : R

Helpful people

Yesterday evening I ran out of ideas on how to implement something in GAP. Intuitively I knew it was possible. Within my understanding of mathematics, anything must bepossible with GAP, I mean GAP is used by professional researchers who speak GAP. Today, when I took a short break at work, I posted my question in the GAP forum. I immediately received two replies and that happened before. There is always someone who helps you out. Somehow that means a lot to me, it's why I believe in the future despite the tremendous problems we have in our world.

Dear Nilo,
You have a ring R, and you want to treat it as a group. This group is
written additively in GAP; so you must convert it to a multiplicative
group first.

Here is a simple example of what you (probably) want to do. Hope it helps:

gap> r := GroupRing(GF(2),SymmetricGroup(3));

gap> rplus := Group(List(Basis(r),AdditiveElementAsMultiplicativeElement));

gap> StructureDescription(rplus);
"C2 x C2 x C2 x C2 x C2 x C2"
--
Laurent Bartholdi \ laurent.bartholdi*****com
EPFL SB SMA IMB MAD \ Téléphone: +41 21-*******
Station 8 \ Secrétaire: +41 21-*******
CH-1015 Lausanne, Switzerland \ Fax: +41 21-*******

Thanks again Mr. Bartholdi.

GroupRing(ZmodnZ(9),CyclicGroup(5))

The SAGE Notebook interface has been updated. It is now possible to select the computeralgebra dialect from a dropdownlist including gap, mathematica, maple and singular, well, basically everything out there except Cocoa perhaps. Besides that, it is possible to use lisp and python as programming languages within SAGE.

To the point, as I was playing a bit in SAGE to get a feeling for the interface I managed to create the following beast.

RG:=GroupRing(ZmodnZ(9),CyclicGroup(5))
free left module over (Integers mod 9), 
and ring-with-one, with 1 generators
Size(RG)
59049

Definitely a beast to my liking.

Implementing change (2)

Daily ( evening / weekend ) study is a process I have to manage carefully, it's my life, basically. Earlier this month I wrote that I have been keeping track of various metrics regarding my study. Well, I tried. Up until now staying motivated and making a sufficient number of hours has been my prime area of concern. I did manage to record my study hours reasonably accurate so I do have some actual statistics at the moment. As far as the other four metrics are concerned I might even change their definition.
* motivation: study hrs/wk
* focus: SuperMemo statistics ( TBD )
* support: Pipeline statistics ( TBD )
* success: ( not defined yet )
* efficiency. ( not defined yet )
Motivation dropped to 63% last week.

Topology

Let X be any set and let T be a family of subsets of X. Then T is a topology on X if
- both the empty set and X are elements of T,
- any union of elements of T is an element of T, and
- any intersection of finitely many elements of T is an element of T.
If T is a topology on X, then X together with T is called a topological space.

Example:
X = {a,b,c} is a set.
T = {0, {a,b,c}, {a,b}, {a,c}, {b,c}. {a}, {b}, {c} } is a family of subsets.
[X, T] is a topological space.

From "Topology Without Tears" by

Sidney A. Morris.

Maximal ideal

Let R be a ring with identity. A proper ideal I ⊆ R is a maximal ideal if I is not a proper subset of any other ideal of R.

All maximal ideals are prime ideals. If R is commutative, an ideal I ⊂ R is maximal if and only if the quotient ring R is a field.

Example:
Let m, n be ideals of Z.
I = (6) = {..., -12, -6, 0, 6, 12, 18, 24, ...}
J = (3) = {..., -6, -3, 0, 3, 6, 9, 12, 15, ...}
The ideal m is not maximal because I ⊂ J, while J is maximal because there is no ideal K such that J ⊂ K.

Ideals in Z

Let I,J be ideals in Z.

If I=(m), J=(n) then I+J=(GCD(m,n)), and I∩J=(LCM(m,n)).

Elliptic Curves

It has been a while but I had another of those euphoric a-ha moments. I have seen a glimpse of what's all the fuzz on Elliptic Curves about. Yes, they are spectaculair.

( More later. )

LaTeX IDE's: shortlist

I have been looking at various LaTeX editors. The cycle of producing mathematics documents is very similar to producing (Java) software so LaTeX editors are in fact complete IDE's. That's why both NetBeans and Eclipse, popular Java IDE's have a LaTeX module ( NetBeans) or plug-in(s) ( Eclipse ).
I have looked at
* Lyx
* TeXnicCenter
* LaTeX for NetBeans
* TeXlipse (Eclipse plug-in)
* LEd

Lyx tries to be wysiwyg, and therefore does not work for high level math. TeXnicCenter is the tool I have been using from the beginning. Excellent, really, but it lacks features like code-folding. LaTeX for NetBeans. It would be extremely cool to be able to produce math in NetBeans. It can be done but the feature set does not even come close to TeXnicCenter, although it has code-folding. TeXlipse is worse than LaTeX for NetBeans. The document structure viewer does not even support multiple file documents. There is something like the Full LaTeX view but it does not work in many cases. LEd. Excellent stuff but it is not very friendly to projects created with other tools. I was not able to import an existing set of tex files.

My choice is TeXnicCenter.

Implementing change

Since the beginning of March I keep track of various metrics regarding my study. It's a way of staying focused. The set of metrics I used was just a try-out. I changed the metrics a bit today. As long as it serves my purpose.
* motivation: study hrs/wk
* focus: repeat-sessions;
* support: new repeat-items
* success: #exercises done
* efficiency. (not defined yet)
A sort of personal CMM.
* 'Motivated'
* 'Focused'
* 'Supported'
* 'Successful'
* 'Efficient'
I am motivated and working on the other levels to achieve. I need to focus more on actually 'doing' math, solving problems, doing exercises and proofs and writing papers. Not to publish them but to get experienced in the mechanics of it. Writing beautiful TeX to start with. I have more than enough ideas, things I want to research. More on that later. - Exercises: I found a few exercises on Rings and Fields, with answers, and here is another set. It is my goal to do most of them in the forthcoming month.

Fermat's Last Theorem

In about 1630 Fermat was reading a recently published translation of Arithmetica by Diophantus of Alexandria. He was making notes in the margin and at one point he entered:

To divide a cube into two other cubes, a fourth power or in general any power whatever into two powers of the same denomination above the second is impossible, and I have assuredly found an admirable proof of this, but the margin is too narrow to contain it.

Today I have seen the documentary about the Andrew Wiles' proof of Fermat's theorem. ( Link to video: [ here ] )

Cornucopia

As seen on MathWorld ( Click and drag )

name="input_archive" value="zip/cornucop.zip" />

alt="Cornucopia" />

SAGE

I downloaded and watched a colloquium on SAGE by William Stein. Stein talks about the past, present and future of SAGE. He is very much in favor of open source software but couldn't find the perfect open source math program so he decided to write one himself. His plan was to reverse-engineer existing open source code and port it to a new Python program. He soon realized it would take several lifetimes to implement so he used existing software as a sort of library behind GAPE. ( ... )

He briefly mentioned none of the open source programs are in any way multi-threaded. I suppose that's both a technical and mathematical challenge. Interesting...

Beware of ignorance ( or: just discovered SAGE )

Ignorance is a lack of knowledge. Ignorance is also the state of being ignorant or uninformed.

Until today I never heard of SAGE. ( ... )

What's so special about SAGE? From the website:

Use SAGE for studying a huge range of mathematics, including algebra, calculus, elementary to very advanced number theory, cryptography, numerical computation, commutative algebra, group theory, combinatorics, graph theory, and exact linear algebra.

SAGE makes it easy for you to use most mathematics software together. SAGE includes interfaces to Magma, Maple, Mathematica, MATLAB, and MuPAD, and the free programs Axiom, GAP, GP/PARI, Macaulay2, Maxima, Octave, and Singular.

You work with SAGE using the highly regarded scripting language Python instead of an obscure language designed for a particular mathematics program. You can write programs that combine serious mathematics with anything else.

Use SAGE from your web browser, which connects either to a program running on your computer, or a program running elsewhere. With the SAGE notebook you can create embedded graphics, beautifully typeset mathematical expressions, add and delete input, and start up and interrupt multiple calculations.

Introduction to SAGE (pdf)

CoCoA

CoCoA, an algebra package. So there is more than GAP. Comparison of computer algebra systems

Computational Commutative Algebra I

Working on Rotman, Chapter 3: 'Commutative Rings I', I often scan ahead. Today I looked at Computational Commutative Algebra 1.

"... This is one of the most refreshing mathematical books I have ever held in my hands. The authors do not believe in teaching by spreading out the material, but they introduce it via questions and discussions, they explore it in an intuitive fashion, exercise it through well-chosen examples, and start the reader on his own expeditions through numerous "tutorials", i.e., guided projects. This is academic teaching at its best: if I had not seen it, I should not have believed that it can be done so well. ... In conclusion, this book gives students a stimulating introduction to commutative algebra very much geared to their need, and it provides numerous useful ideas to those who teach the subject." (H.Stetter, IMN - Internationale Mathematische Nachrichten 2003, Vol. 57, Issue 193)

Books

Some books are to be tasted, others to be swallowed,
and some few to be chewed and digested.
Francis Bacon (1597)

From Artin to Rotman

Every Coin Has Two Sides. I have this corrupt file, including several corrupt backups, which I used to store notes from, and manage Artin's Algebra. The good thing is that I decided to start working in another book.

Mathematica 6 is slow

Fom some expert forum ( non-Wolfram of course )

I also read things said in wolfram forums. The issue is totally different. There is no way to change or play with options. In our case the integral is straight forward with no singularities at all! Something like this:

F[t_]:=NIntegrate[e^t ((a+b)-3a^2 )^8, {a,0,b},{b,0,3}]
Plot[F[t],{t,0,4}]

That's it. No singularities.. no cut-off's nothing. Pure and simple double integral. When you try with v6.0 it does it 5 or sometimes 7 times slower than v5.2.

Let's assume there is something we miss in these calculations.. ok?

Let's go back to Wolfram's built in function called Benchmark; to test how fast it handles 15 various problems. On both versions this command exists. You give a try on both.. you still come out with the result that overall Mathematica 6.0 is slower than Mathematica 5.2.

This is the reality of it. Maybe v6.0 while calculating it also thinks how to decorate the result and show it nicely with colors and so on.. But who needs to wait 5 times more for "loox" as you said, right?

I hope Wolfram will take care of this issue. Meanwhile I will stick to v5.2.
Or even 4.1 which is btw faster than 5.2 :)

Try before you buy, or better wait until 6.1 or so.

Example of a finite vector space

The vector space of dimension 2 over the finite field GF(3) is isomorphic to the abelian group Z3 X Z3.

gap> b:=One(GF(3))*[[1,0],[0,1]];
[ [ Z(3)^0, 0*Z(3) ], [ 0*Z(3), Z(3)^0 ] ]
gap> V:=VectorSpace(GF(3),b);

gap> Dimension(V);
2
gap> Size(V);
9
gap> Elements(V);
[ 
[ 0*Z(3), 0*Z(3) ], 
[ 0*Z(3), Z(3)^0 ], 
[ 0*Z(3), Z(3) ], 
[ Z(3)^0, 0*Z(3) ],
[ Z(3)^0, Z(3)^0 ], 
[ Z(3)^0, Z(3) ], 
[ Z(3), 0*Z(3) ], 
[ Z(3), Z(3)^0 ], 
[ Z(3), Z(3) ] 
]

Wallpaper groups

Wallpaper groups are two-dimensional symmetry groups, intermediate in complexity between the simpler frieze groups and the three-dimensional crystallographic groups (also called space groups).

Discover the wallpaper patterns with the Kali Java applet.

How it's like to remember 22,500 digits of Pi

The Boy with the Incredible Brain ( Channel 5 rip on Google Video )

Remember Max Cohen in the movie Pi when the little child with the calculator asks him to do some difficult calculation? Daniel Tammet, beats Max and Daniel is real. But probably just as mad as Max. His disease is called autism.

I don't believe in his brilliance. If he was so brilliant why does he spend time learning the digits of Pi instead of coming up with some new identities for Pi which will deepen the understanding of Pi in the entire mathematical community? The researchers researching him aren't mathematicians but people who think math and arithmetic are one and the same.

Tammet is clever in the way he exploits his ability. There is nothing wrong with that. I don't expect any breakthroughs in science of him though. The real geniuses are working hard, day and night, far away from the publicity.

In the movie he meets the real Rain Man. He is certainly amazing. When you ask Rainman a questions like: "If Churchill would still live today, how old would he be and on what day of the week would be his birthday?" he answers immediately, and correct, of course.

People like Rainman and Tammet are called savants.

Abstract Algebra

Algebra is a branch of mathematics.

Algebra may also mean:
* elementary algebra
* abstract algebra
* linear algebra
* universal algebra
* computer algebra

In addition, many mathematical objects are known as algebras.

In logic:
* Boolean algebra
* Heyting algebra

In set theory:
* algebra over a set
* sigma algebra

In linear algebra, and the study of vector spaces:
* algebra over a field
* associative algebra
* commutative, anticommutative, and super- algebras
* Lie algebra

In ring theory:
* algebra over a commutative ring (or R-algebra)

In category theory:
* F-algebra
* F-coalgebra

In the relational model:
* Relational algebra

Hilbert's Hotel

The hotel manager David Hilbert had a very large hotel, in fact, it had infinitely many rooms numbered 1, 2, 3, ... The hotel was very popular and every room was occupied. One day a new guest arrived.
-Is there any free room?
-No, Mr. Hilbert said.
-Oh, what a pity, the guest said and started to walk away.
-But wait, you can still get a room.

The new guest was very confused by this and asked how that could be possible.
-I'll just ask the guest in room number 1 to move to room number 2, the guest in number 2 move to room 3, the guest in room 3 move to number 4, and so on, and then you can have room number 1.

The guest was very happy with this and called his friends to tell them about this fantastic hotel. Then one day they all arrived at the same time.
-Hello, we are countably many people, and we want a room each. Mr. Hilbert felt reluctant to ask each guest to move to a new room an infinite number of times. That would be very unpleasant, and they will never finish either. Luckily he got a brilliant idea.
-I'll let guest in number 1 move into number 2, guest in number 2 move into number 4, guest in number 3 move into number 6, number 4 to number 8 and so on. Then you can move into any room with an odd number; they will all be free, and there will be rooms for all of you.

Now all the new guests got a room on their own.

By Daume on PlanetMath

Mathematics Podcast

Check out Math Mutation Podcast for short podcasts for people of all ages, where we explore fun, interesting, or just plain wierd corners of mathematics that you probably didn't hear in school. ( ... You never know what might bring you the next idea you'll be working on. ...)

LEGO Difference Engine

Long before the age of electronic computers, even before Alan Turing invented the theoretical Turing Machine, Charles Babbage invented a mechanical computer which he called the Difference Engine. Andrew Carol rebuilt one using LEGO.


Click to enlarge

Problem ( Group Theory )

Show that, then prove.

Let G be a group in which each proper subgroup is contained in a maximal subgroup of finite index in G. If every two maximal subgroups of G are conjugate in G, then G is a cyclic group.

Group Theory

An introduction to the theory of groups / Joseph Rotman --4th ed.
1995 Springer Verlag ISBN 0-387-94285-8




More is less. While browsing through this book I realized how little I know about the subject. How long will it take before I can conider myself 'current' in the field? And that's only Group Theory. There are a few other topics I would like to know more about... - Every Coin Has Two Sides. The other side of the coin of fascination is fear.

The magic of PI

Download the Pi poster in PDF format below and start zooming in, you'll find the first 350,390 digits of Pi on one single page. The power of what you can do with PDF.

Lie Group E8

From Science Daily:

Mathematicians have mapped the inner workings of one of the most complicated structures ever studied: the object known as the exceptional Lie group E8. This achievement is significant both as an advance in basic knowledge and because of the many connections between E8 and other areas, including string theory and geometry.

Lang or Artin?

Although I still have decades of stuff to cover before I can really compare Lang and Artin I do have an opinion. Those who studied either or both of them seem to agree on one thing: neither of the books should be used as a text for a course, let alone for self-study: they are works of reference. Now that's strange because at least Artin's book was written from many years of course notes. I think the books should be studied but with many companion books to help you get through. Artin wrote in the preface: "...Sometimes the exercise of deferring material showed that it could be deferred forever - that it was not essential. This happened with dual spaces and multilinear algebra. ..." I tried to start reading Representation theory, by Fulton and Harris with nothing more than an undergraduate abstract algebra introduction as preparation. I couldn't finish the book because it was packed with topics from multilinear algebra. - I have been warned, warned and warned to take it easy but I go for Lang, why not? Mathematics grew into my fascination and passion. What else can I do?

How much is 25 divided by 5 ?

25 divided by 5? That's 14 each. 25/5 = 14.