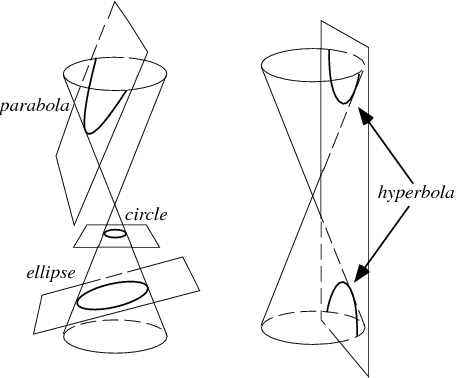
A conic section is an affine variety like V(x^2 + y^2 - z^2, ax + by + cz). Where x^2 + y^2 - z^2 = 0 is the equation of a cone and ax + by + cz = 0 is the equation of a plane in three dimensional affine space. Depending on the values of a, b and c the affine variety takes the form of a circle, ellips, parabola or hyperbola.
Interesting, not? Let's experiment in Mathematica.
Show[
ContourPlot3D[x^2 + y^2 - z^2, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}],
ContourPlot3D[-2x + y - z, {x, -2, 2}, {y, -1, 1}, {z, -2, 2}]
]

This images almost asks to be rotated in 3D for further visual inspection. This is where the superb JavaView comes in but that is something for another time.









No comments:
Post a Comment